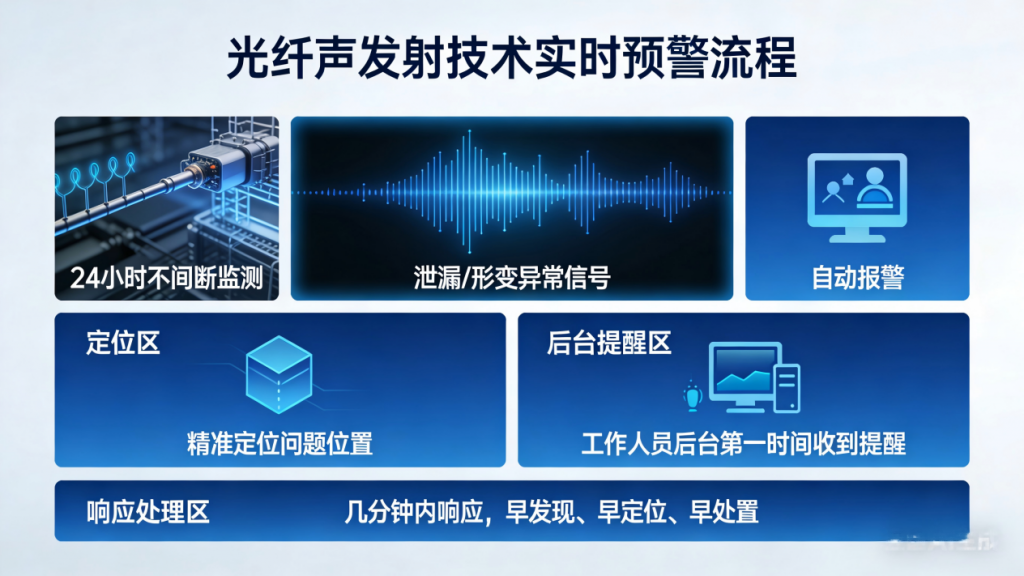
一、时域与频域
在时域分析中,以时间为横轴,信号的幅度为纵轴,绘制出信号的波形图。通过这个波形图,可以清晰地获取到信号的许多基本信息。如信号的幅值,它代表了信号在某个时刻的强度大小;周期表示信号重复变化的时间间隔;脉冲宽度表示脉冲信号持续的时间长短。这些信息对于初步了解信号的特征非常重要。
图为声发射信号的时域图:
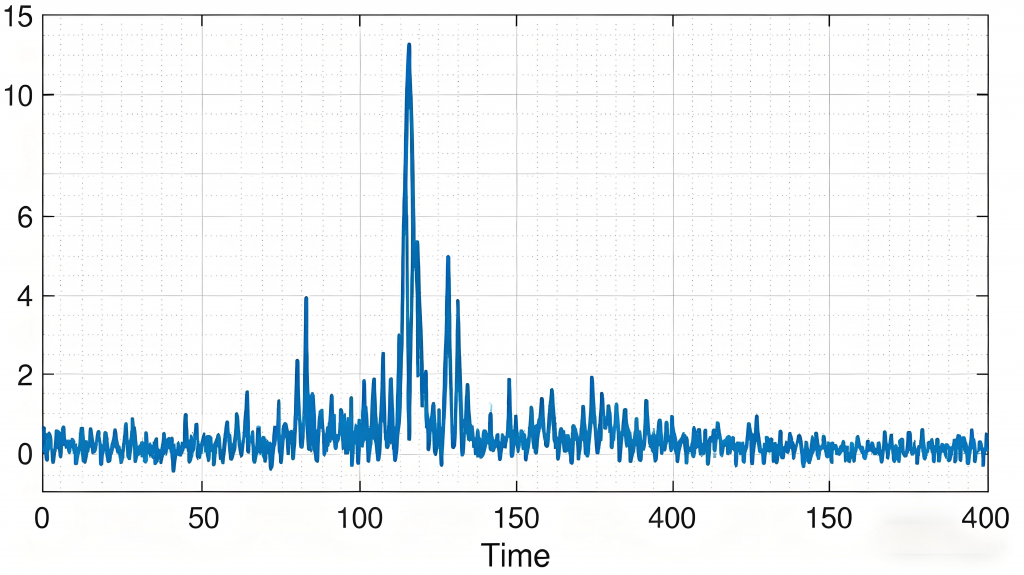
从图中可以观察到信号包含多个脉冲,其中最大脉冲(幅值约14)是显著特征,后续脉冲幅值随时间衰减(如第二个脉冲幅值约4)。脉冲在时间轴上非均匀分布,最大脉冲后脉冲密度增加,后续脉冲幅值持续降低,呈现“先突变后衰减”的时域趋势。
若需要观察声发射信号的频率组成,则需要通过频域分析来完成。频域分析通过傅里叶变换将信号从时域转换到频域,以频率为横轴、幅度或功率为纵轴展示信号特性。这样可以清晰看出信号中包含哪些频率成分及其强弱分布。
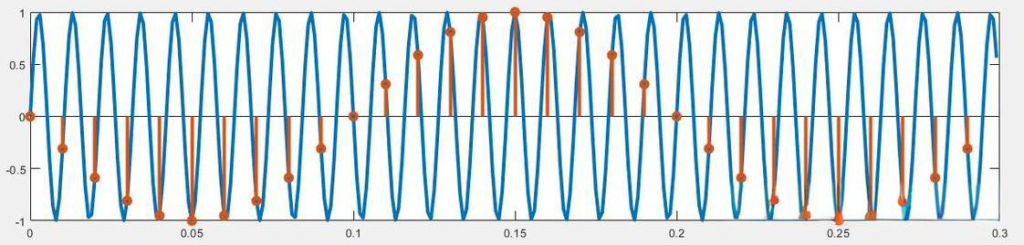
下图第1幅图是时域图,第2-3幅图是频率图。
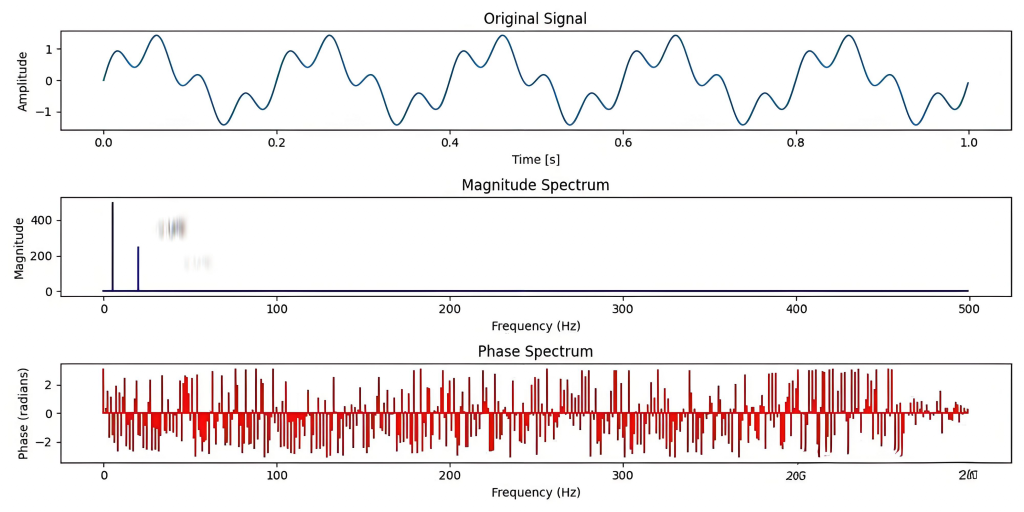
时域信号分析
观察Original Signal子图,信号为周期性波动的时域波形:
振幅:波形在正负方向有明显起伏,反映信号随时间的强度变化;
周期性:波形呈现规律重复的波动形态,体现信号的周期特性。
频域信号分析
频域信号通过傅里叶变换将时域信号分解为不同频率的分量,包含幅度谱与相位谱两部分:
幅度谱(Magnitude Spectrum)
频率分布:幅度谱中仅在低频区域(频率轴左侧)存在显著峰值,说明信号的主要能量集中在低频分量;
能量集中度:高频区域幅度极低,反映信号高频成分稀少,能量高度集中在低频段。
相位谱(Phase Spectrum)
相位分布:相位谱在低频区域(与幅度谱峰值对应)呈现规律的相位变化,高频区域相位波动幅度大;
物理意义:相位谱反映各频率分量的相位关系,低频分量的相位规律性与幅度谱的能量集中性一致,高频分量的相位波动可能由噪声或信号细节引起。
二、傅里叶变换
具体的数学公式为:对于一个时域信号f(t),其傅里叶变换F(ω)可表示为:
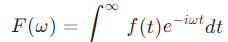
这里的e^-iωt可以看作是一个频率分析器,它能将信号f(t)按照不同的频率f(t)进频率ω进行分解,F(ω)则是信号在频域的表示,它反映了信号中各个频率成分的强度和相位信息。
下图是傅里叶级数的直观可视化:
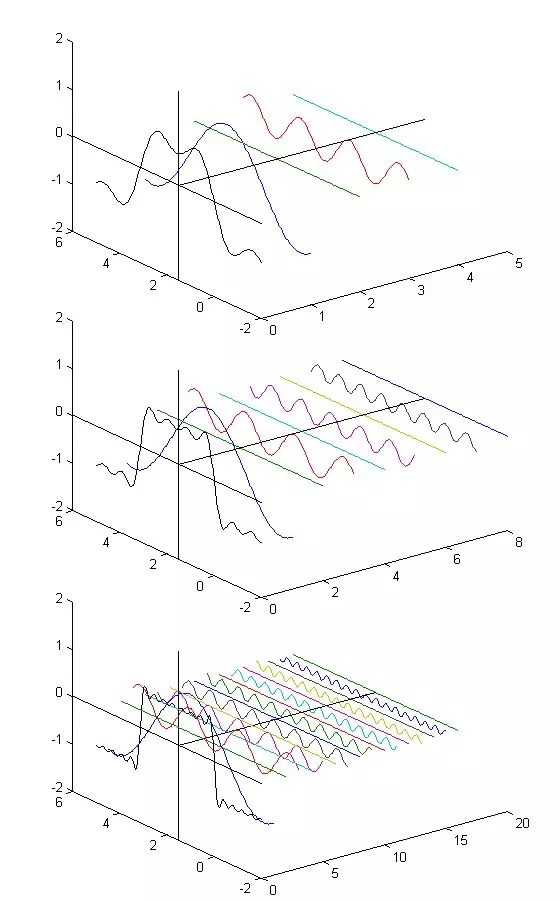
任何周期性函数(如矩形波)都可以分解为一系列不同频率、不同振幅的正弦波(和余弦波)的叠加。
从这三幅图的变化可以看出:
随着参与叠加的正弦波分量数量增多,最前面的合成波(黑色)越来越接近理想的矩形波。这体现了傅里叶级数的“收敛性”—— 分量越多,逼近程度越高。
那些 “振幅为 0 的直线”,对应傅里叶级数中系数为 0 的频率分量。这说明矩形波的傅里叶展开只包含特定频率(基频的奇数倍)的正弦波,其余频率分量的贡献为 0。
三、声发射信号时域和频域分析案例
当轴承在运行过程中出现故障时,如裂纹、磨损等,会在故障点产生微小的形变或振动,这些形变或振动会以弹性波的形式传播出来。通过安装在轴承附近的声发射传感器,可以捕获到这些弹性波信号,并将其转换为电信号进行后续的分析和处理。
轴承故障的声发射检测流程通常包含以下几个步骤:
1、采用高灵敏度声发射传感器及配套数据采集装置对轴承进行声发射信号采集;2、对原始信号实施预处理操作,通过滤波、降噪等技术手段提升信号信噪比;
3、对预处理后的信号进行特征提取与模式识别,以辨识出与轴承故障相关的特征信号;
4、基于特征信号分析结果,对轴承的故障类型、位置及严重程度进行诊断与评估。
下图为轴承在转速2977 r/min下的时域信号以及频域信号:
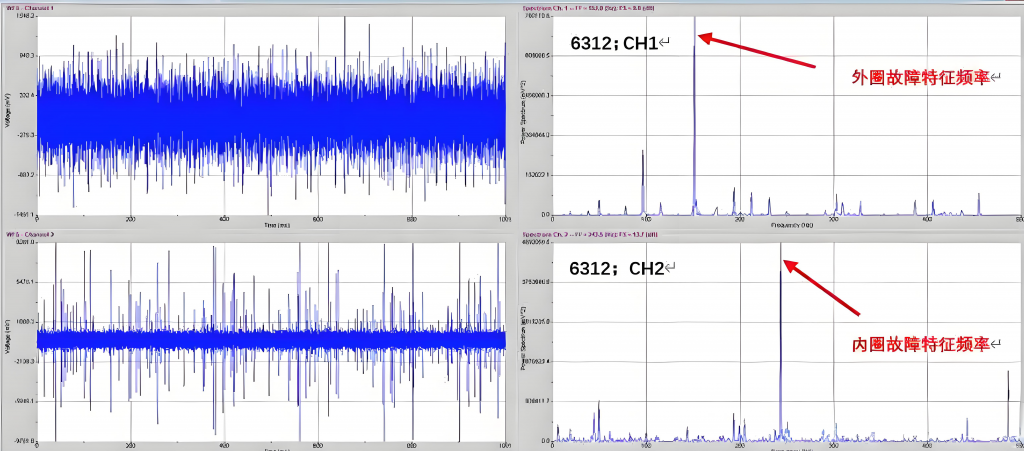
通过对采集到的波形流进行时域、频域分析发现:
CH1时域波形呈现周期性冲击脉冲,对应轴承外圈剥落等故障时的冲击振动,特征频率为152Hz,该频率与外圈故障频率完全吻合,可初步断定轴承1为外圈故障。
CH1时域波形同样存在周期性冲击,反映内圈故障(如剥落、磨损)引发的振动特征。特征频率为243.5Hz,该频率与内圈故障频率非常接近,可初步断定轴承2为内圈故障。