一、采样精度
采样精度,也称作采样位数,它是在采样过程中,用于衡量每个采样点数值所能表示的位数。简单来说,它反映了对模拟信号幅度的量化精细程度。
在声发射信号采集领域,常用的采样精度有16bit和18bit。可以把采样精度想象成一把尺子,尺子上的刻度越细密,测量就越精准。
16bit 的采样精度意味着可以将模拟信号的幅度划分成2^16=65536个不同的量化等级,而 18bit 则能划分成2^18=262144个量化等级。这就好比用一把刻度更密的尺子去测量物体,18bit比16bit 能够更细致地区分信号幅度的微小差异,从而更精确地还原原始信号的幅度信息。
二、采样精度对采集信号的影响
采样精度在很大程度上决定了记录信号的动态范围和保真度。
动态范围是指信号能够表示的最大幅度与最小幅度之间的差值。采样精度越高,可表示的量化等级越多,能够记录的信号动态范围也就越大,对信号的保真度也就越高,越能保留原始信号的细节和特征 。
我们以音频信号为例来理解这个概念。
在数字音频中,16bit 采样精度是CD音频的标准,它能够提供较为出色的音质,满足大多数普通听众的需求。
而在专业音频录制和制作领域,常常会采用 24bit 甚至更高的采样精度。因为在录制一些细微的声音,比如乐器的微弱泛音、歌手气息的轻微变化时,高采样精度可以更精准地捕捉到这些细节,使得录制出的音频更加真实、细腻,还原度更高 。
将其类比到声发射信号采集上,如果采样精度较低,当遇到一些幅度较小但对材料状态判断至关重要的声发射信号时,可能无法准确分辨其幅度变化,导致信号细节丢失。
如在监测金属材料裂纹萌生初期,裂纹产生的声发射信号幅度相对较小,如果采样精度不足,这些微弱信号可能就会被忽略或者记录不准确,进而影响对材料损伤状态的判断。
相反,高采样精度能够清晰地捕捉到这些微弱信号的幅度变化,为后续分析提供更丰富、准确的信息,有助于更及时、准确地发现材料内部的早期损伤 。
三、采样精度实际应用考量
在实际应用中,选择合适的采样精度并非越高越好,而是需要综合多方面因素来考虑。
首先要考虑传感器的可分辨信号。一般来说,声发射传感器都有其能够分辨的最小信号幅度,若采样精度远超传感器的分辨能力,就如同用高精度显微镜去观察一个本身就很模糊的图像,即便显微镜精度再高,也无法获取更多有效信息,反而会增加数据处理的负担和成本 。
系统电气噪声也是不可忽视的因素。任何电气系统都会存在一定的噪声,这些噪声会对采集到的声发射信号产生干扰。如果采样精度过高,而系统噪声又相对较大,那么噪声信号可能会被错误地当作有效信号进行量化记录,从而影响信号的准确性。
例如,当系统的电气噪声幅度与声发射信号中一些微弱信号的幅度相当,且采样精度过高时,噪声信号就可能会被误判为有效信号,导致数据分析出现偏差 。
环境噪声同样会对采样精度的选择产生影响。在实际监测环境中,周围环境的噪声可能会混入声发射信号中。
通常,检测与试验门限会设置在一定的分贝值以上,以过滤掉部分环境噪声。如果采样精度选择不当,可能会将环境噪声误判为有效信号,或者无法准确记录真实的声发射信号。
所以,在实际应用中,需要根据传感器可分辨信号、系统电气噪声和环境噪声等因素,综合评估来选择合适的采样精度,以确保既能准确采集到有用的声发射信号,又不会因过度追求高精度而带来不必要的资源浪费。
四、采样率
采样率是指在单位时间内,对模拟信号进行采样并完成 AD 转换的数据点数,其单位通常为赫兹(Hz)。
简单来说,它就像是给连续变化的模拟信号拍照,采样率就是每秒拍摄的照片数量。
采样率与信号频率之间存在紧密的联系,根据奈奎斯特采样定理,为了能够无失真地还原原始信号,采样率必须不低于原始信号最高频率的两倍。
如果采样率低于信号最高频率的两倍,就会出现混叠现象,导致高频信号被错误地表示为低频信号,使得原始信号无法被准确重建。
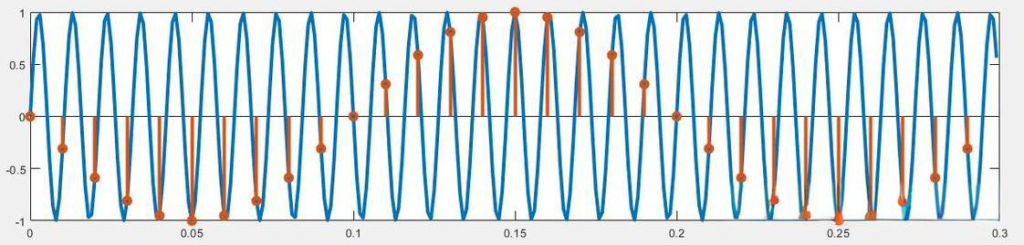
例如,当用Fs=100HZ的采样频率,对100Hz的正弦波信号进行采样时,其情形就如下图中棕色采样点所示,连接起来是一个虚假的5Hz正弦波信号。
五、采样率对采集信号的影响
采样率对信号的还原程度有着直接影响。一般而言,采样率越高,在单位时间内采集到的数据点就越多,对信号时间变化的捕捉就越精细,能够更准确地还原原始信号的波形,所采数据的失真也就越小。
我们可以通过一个简单的公式和实例来更直观地理解。假设我们有一个频率为f的正弦信号,采样率为s,重构波形峰值偏离实际信号峰值的偏离时间为t,被测信号的周期为T(T=1/f), n=s/f 测量幅度误差为dA,则有:
dA = 1 – cos(2πt/T)
进一步推导可得:
dA = 1 – cos(πf/s)
以一个 400KHz 的正弦信号为例,当采样率为 1000KHz(即 1000kSample)时,根据公式计算可得:
dA = 1 – cos(π*400/1000) ≈ 0.309017
对应的幅度误差:
A(dB) = 20lgdA ≈ -10.2004dB
当采样率提高到 2000KH时:
dA = 1 – cos(π*2000/1000) ≈ 0.809017
对应的幅度误差:
A(dB) = 20lgdA ≈ -1.84085dB
可以明显看出,随着采样率的提高,幅度误差显著减小,信号的还原度更高。
采样率的提高虽然能提升信号采集的质量,但也会带来数据量的急剧增大。
因为单位时间内采集的数据点增多,需要存储和处理的数据量也相应增加,对存储设备的容量和数据传输的带宽和处理速度都带来了巨大挑战。
在实际应用中,如果系统的存储和处理能力有限,过高的数据量可能会导致数据丢失增多,反而影响信号采集的效果。因此在选择采样率时,需要在信号失真程度和数据量之间找到一个平衡点,以确保既能满足信号采集的精度要求,又能保证系统的正常运行。
六、采样率在不同场景的应用
在实际的声发射信号监测应用中,不同的场景对采样率有着不同的要求,需要根据具体情况进行合理选择。
岩石检测领域
岩石内部裂纹扩展等产生的声发射信号频率多在几十KHz,信号频率相对较低,根据奈奎斯特采样定理,实际 5M 采样率即足够满足要求,在实际检测中一般将采样率设置在 2M 以下。这样既能保证准确捕捉到岩石声发射信号的特征,又不会因为过高的采样率产生过多冗余数据,增加不必要的成本和处理负担。
金属损伤检测
金属材料的特性以及损伤产生的声发射信号特点与岩石有所不同。金属在受到外力作用发生塑性变形、裂纹萌生和扩展时,产生的声发射信号频率范围较宽,可能会包含一些高频成分 。对于一些高频信号占比较大的金属损伤检测场景,就需要更高的采样率来确保能够准确采集到信号的全部细节。
例如,当检测某些高速冲击下的金属材料损伤时,信号中可能存在数MHz 的高频成分,此时就需要采用 10M 甚至更高的采样率,以避免信号混叠和失真,从而为准确判断金属的损伤状态提供可靠的数据支持。
航空航天领域
对飞行器结构的声发射监测至关重要。飞行器在飞行过程中,结构部件承受着复杂的力学载荷,任何微小的损伤都可能引发严重的安全事故。
这里的声发射信号不仅频率范围广,而且信号特征复杂多变。为了及时、准确地捕捉到飞行器结构损伤产生的声发射信号,需要根据不同部件的工作状态和可能产生的信号频率,动态调整采样率。
对于机翼等关键部位,在飞行过程中可能会受到强烈的气流冲击和振动,产生的声发射信号频率较高且变化迅速,就需要设置较高的采样率,如 20M – 40M ,以保证能够实时监测到结构的微小变化。
对于一些低频振动信号较多的部件,采样率则可以适当降低,但也需要满足奈奎斯特采样定理的要求,以确保信号采集的有效性 。